

Interestingly enough, we can attempt to apply the Koide formula to these six masses - in two separate groupings - to see what comes out. Using the best data presently available, their masses (shown without uncertainties) are: The first three are the lightest quarks, the latter three are the heaviest quarks. Plenty of suggestive, tantalizing relationships have turned out to be nothing more than coincidences.Īnd yet, we have precisely measured values for not only the charged leptons, but for each of the quarks as well: the up, down, strange, charm, bottom, and top quarks.
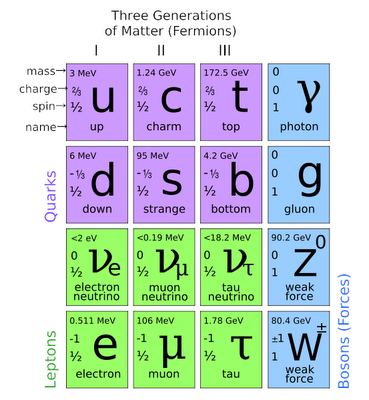
Today, however, it’s measured to be 1/137.0359991, and it’s known to increase in strength at higher energies: up to ~1/128 at electroweak scales. In the early days, people thought the fine-structure constant might be exactly equal to 1/136 a little later, that was revised to 1/137. Now, there are many, many relations that one can cook up between various numbers or values that aren’t actually representative of an underlying relationship, but merely appear as a numerical coincidence. be inserted into the formula, guaranteeing a result between 1/3 and 1, the fact that the result is right in the middle, at 2/3 to the limit of our experimental uncertainties, suggests that there might be something interesting to this relation. The Koide formula, as applied to the masses of the charged leptons. In the case of these charged leptons, it just happens to itself be a simple fraction: ⅔, almost exactly. Which mathematically must lie between ⅓ and 1. and divide their sum by the square of the sum of their square roots,.that if you add the three relevant masses together,.And it’s that same mathematical structure that Koide leveraged when he proposed a very simple formula: Although this isn’t necessarily applicable to the masses of the charged leptons (or any particles at all), it’s a possibility that might be worth exploring. Perhaps it’s just a numerical coincidence, but it’s well known - at least, in quantum physics - that whenever two particles have identical quantum numbers, they’re going to mix together at some level you’ll have a mixed state instead of a pure state. The tau - the third-generation counterpart of the electron and muon - is similar but even heavier and shorter lived, with a mass that’s about 17 times the muon’s mass and a mean lifetime of just ~290 femtoseconds, surviving less than one-millionth the amount of time a muon lives for. The muon, its heavier cousin, is identical in terms of electric charge, spin, and numerous other quantum properties, but its mass is ~207 times greater, and it’s fundamentally unstable, with a mean decay lifetime of ~2.2 microseconds.

The electron is the lightest charged particle in the Standard Model, and the lightest of all massive particles except for the neutrinos. Here, as was its original intent, it's applied to the charged leptons: the electron, muon, and tau particles. three particles that obey its particular mathematical relationship. A geometrical interpretation of the Koide formula, showing the relative relationship between the.


 0 kommentar(er)
0 kommentar(er)
